Which part should be filled?
When we draw a simple shape like a square or a circle and we are told to fill the shape, it is very easy to determine what is inside the shape and therefore what we should fill.
However, as shapes become more complex with the shape's drawing paths intersecting multiple times, it becomes unclear as to whether different segments of the shape should now be considered as "inside" of the shape or "outside" of the shape.
When using the Canvas API and we draw shapes like this and then use the methods fill(), clip() or isPointInPath(), it is important to understand how to calculate the "inside/outside" characteristic of the different segments in a shape, and therefore fully understand why the canvas fills/crops the shape in a specific way and/or how we can adjust it our needs.
The <canvas> like many other computer graphical programs uses a concept called the winding rule which is a technique that determines whether segments of a shape are "inside/outside".
There are two kinds of windings called the non-zero winding rule and the even-odd winding rule. The by default will use the non-zero winding rule. For the purpose of this article and understanding the difference between the two winding rules we will use the fill() method.
We can switch the winding rule by passing a different winding rule name into the fill() method.
fill('nonzero') - Fill a shape using the non-zero winding rule (default)
fill('evenodd') - Fill a shape using the even-odd winding rule
We have drawn two relatively complex paths, one that we have filled with a yellow fill and one that we have filled with a red fill. Taking a brief look at the two shapes, the key difference is that the small square that has been created at the intersect of the two larger squares is filled for the yellow shape and not-filled for the red shape.
The Yellow Shape (non-zero winding)
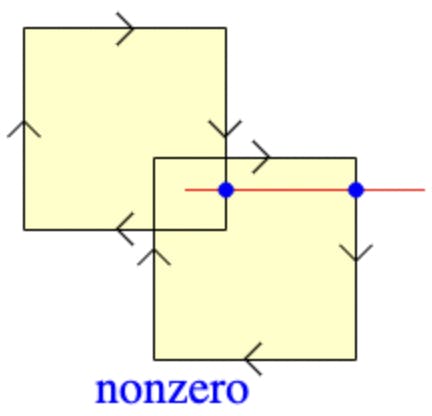
The yellow shape is using the default canvas fill rule of 'nonzero'. This technique calculates whether a region lies inside the shape or outside the shape by drawing a straight reference line from inside the region that we are calculating to a sufficiently distant position that we can confidently say is outside the shape. We then examine the points where the reference line intersects with the shape's paths and create a score or winding number based on whether at the intersect points the shape's path was drawn using a clockwise stroke or anti-clockwise path. Each time the reference line intersects with a clockwise path we subtract 1 from the winding number. Each time the line intersects with an anti-clockwise path we add 1 to the winding number. After examining all the intersect points along the reference line, we will have a winding number that is either greater than zero, less than zero or equal to zero. If the winding number is greater than or less than zero, we can say that the score is non-zero and therefore the region is classed as inside the shape and should therefore be filled. If the winding number is equal to zero, the region is classed as outside the shape and should not be filled.
winding number !== 0 - region is inside shape and should be filled
winding number === 0 - region is outside shape and should NOT be filled
To illustrate this we have drawn two blue dots for the points of intersect between the reference line and the yellow shape's paths. Starting at the central region and looking at the blue dot on the left. The path at this point is clockwise and so the winding score is -1. Next, looking at the blue dot on the right, we can see that the path is also clockwise and so the winding score is now -2. -2 is less than zero so the region is classed as inside the shape and should be filled.
The Red Shape (even-odd winding)
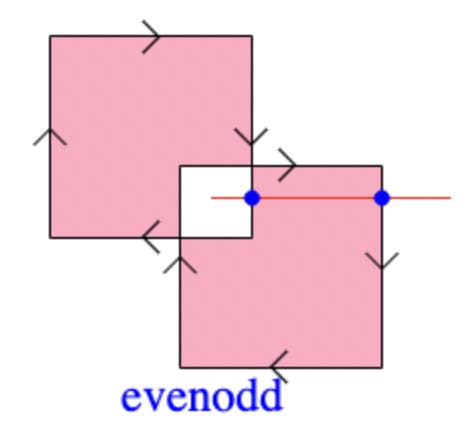
The red shape is using the canvas fill rule of 'evenodd'. This technique also uses a reference line drawn from the region we are trying to calculate to a remote distant point. Again we look at the points where the reference line intersects with the shape's paths. This time we simply count the number of intersections and determine whether the total number of intersections is even or odd. If the total count is odd, then we say that the region is inside the shape. If the total is even, then we say that the region is outside the shape.
odd number of intersections - region is inside shape and should be filled
even number of intersections - region is outside shape and should NOT be filled
To help explain this we have drawn two blue dots at the points of intersect between the reference line and the shape's paths. We can only count 2 points of intersection. The total is even so we can say that the region is outside of the shape and therefore should not be filled.
Have a play around with the code lab below.
I have to put my pen down now. 🤸♂️
